Turning a convex partition into a Voronoi diagram
 [New wiki page on Voronoi diagrams]
[New wiki page on Voronoi diagrams]A Voronoi diagram (named after Russian mathematician Georgy Voronoi, 1868-1908) is a partition of space based on a set of points. This is the main idea: we are given a set - usually small and sparse - of points which we'll call Voronoi centers. Let's suppose that each of these center points has its own color. Then we can color all of space by coloring any point according to the center it is closest to.
In the figure here (from wikipedia), each black dot is a Voronoi center, and the cells are colored accordingly.
It's easy to think of some places where we might see similar patterns in nature. For example, the shapes on a turtle's shell, or the hexagons of a honeycomb resemble Voronoi diagrams. Close-packed living cells sometimes do as well, maybe because as they became further squished together, their boundaries approached a shape optimized for packing.

You might notice that every cell in a Voronoi diagram is convex - it is a shape without "dents" - every line between two points in a Voronoi cell is contained within that cell (contrast this with, say, pac man). So every Voronoi diagram is a convex partition. Is every convex partition also a Voronoi diagram? No! In fact, there are many ways to draw a convex partition which is impossible to represent as a Voronoi diagram (see the wiki for some details).
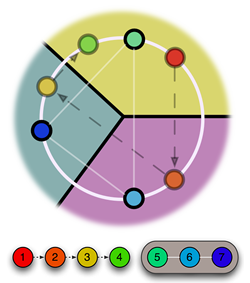
But for those convex partitions which allow a Voronoi diagram, how hard is it to find the corresponding center points? With the right algorithm, it's not so difficult. Here's the main idea: draw a circle around some intersection of three boundaries in the convex partition, pick a random point, and reflect it around the boundaries. After reflecting three times, take the average of this point, and the starting point, along the circle. What you get is a working Voronoi center for that intersection. Reflect this point around to find the other two centers (if you reflect it three times, you'll just get back to your original point). Check out the figure.
Once we have candidate Voronoi centers for any two adjacent 3-intersections, you can expand the circles on which these centers exist until the centers line up. These centers are guaranteed to be the correct unique center for their cells (assuming that the convex partition is a Voronoi diagram). From here, just reflect the centers over the neighboring boundaries of the partition to find all other centers.
This is just a quick summary of a few of the thoughts on the wiki page.

